某人独立地射击10次，每次射击命中目标的概率为0.8，随机变量X表示10次射击中命中目标的次数，则E(X
)等于( )．
)等于( )． 正确答案：
B
答案解析：
解：把每次射击看成是做一次伯努利试验，"成功"表示"命中目标"，"失败"表示"没有命中目标"，出现成功的概率p=0.8．于是，X服从参数n=10，p=0.8的二项分布．已知二项分布的数学期望与方差分别是
E(X)=np=10×0.8=8，
D(X)=np(1-p)=10×0.8×0.2=1.6.
于是，由方差的计算公式推得
E(X)=D(X)+［E(X)］=1.6+8=65.6.故选(B).
本题借助于常用分布的数字特征来求E(X)是比较方便的，因为常用分布的数学期望与方差可以作为已知值使用．如果用随机变量函数的数学期望的定义，即
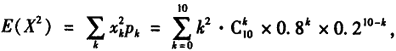
则加法不易计算．
E(X)=np=10×0.8=8，
D(X)=np(1-p)=10×0.8×0.2=1.6.
于是，由方差的计算公式推得
E(X
)=D(X)+［E(X)］=1.6+8=65.6.故选(B).本题借助于常用分布的数字特征来求E(X
)是比较方便的，因为常用分布的数学期望与方差可以作为已知值使用．如果用随机变量函数的数学期望的定义，即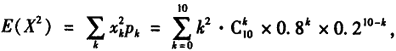则加法不易计算．